Clase XII (Viernes 02 de diciembre del 2016)
- Se realizó la evaluación N°2
Si deseas ver la evaluación, dirigete a EVIDENCIAS.
Clase XIII (Miércoles 07 de diciembre del 2016)
- EVENTOS INDEPENDIENTES:
Sean A y B eventos cualesquiera de un espacio muestral S. Se dice que A y B son independientes si P(A|B) = P(A) y P(B|A) = P(B), es decir que el evento A no depende del evento B y el evento B no depende del evento A.
Lo anterior es equivalente a la siguiente definición:
Definición: Eventos Independientes
Lo anterior es equivalente a la siguiente definición:
Definición: Eventos Independientes
A y B son eventos independientes si P(A∩B) = P(A) P(B)
Demostración:
De la definición de
probabilidad condicional,
P(A|B) =
P(A∩B)/P(B), P(B)≠0
Si A y B son
independientes: P(A|B) = P(A).
Si se sustituye en
la fórmula de probabilidad condicional:
P(A) = P(A∩B)/P(B)
Se obtiene el la
fórmula en la definición
- Realización de
ejercicios:
Ejercicio 1
Calcule la
probabilidad que el último dígito del número de una placa de carro
elegida al azar sea par y el penúltimo dígito sea impar.
Sean los eventos:
A: El último digito
es par
B: El penúltimo
dígito es impar
Cada evento no está
relacionado con el otro evento, entonces son independientes.
Por lo tanto, P(A∩B)
= P(A) P(B) = 0.5 x 0.5 = 0.25
Ejercicio 2
En una caja hay 10 baterías de las cuales 4 están en buen estado. Se repite dos veces el siguiente ensayo: extraer una batería al azar, revisar su estado y devolverla a la caja.
a) Encuentre la probabilidad que en ambos intentos se obtenga una batería en buen estado.
Sean los eventos:
A: La primera batería que se toma de la caja está en buen estado
B: La segunda batería que se toma de la caja está en buen estado
Este tipo de experimento se denomina: Muestreo con Reemplazo.
La primera batería se toma de la caja y se la devuelve, entonces el evento B no es afectado por el resultado que se obtuvo en el evento A, por lo tanto son eventos independientes.
P(A∩B) = P(A) P(B) = 0.4 x 0.4 = 0.16
b) Calcule la probabilidad que en los dos intentos se obtenga al menos una batería en buen estado.
Con la conocida Fórmula Aditiva de Probabilidad,
a) Encuentre la probabilidad que en ambos intentos se obtenga una batería en buen estado.
Sean los eventos:
A: La primera batería que se toma de la caja está en buen estado
B: La segunda batería que se toma de la caja está en buen estado
Este tipo de experimento se denomina: Muestreo con Reemplazo.
La primera batería se toma de la caja y se la devuelve, entonces el evento B no es afectado por el resultado que se obtuvo en el evento A, por lo tanto son eventos independientes.
P(A∩B) = P(A) P(B) = 0.4 x 0.4 = 0.16
b) Calcule la probabilidad que en los dos intentos se obtenga al menos una batería en buen estado.
Con la conocida Fórmula Aditiva de Probabilidad,
P(A∪B) = P(A) + P(B) – P(A∩B) = 0.4 + 0.4 – 0.16 = 0.64
Si deseas conocer más acerca de eventos independientes, dale click AQUÍ.
Monterey Institute, (2012). Probabilidad de eventos independientes. Recuperado 07 diciembre 2016 de: http://www.montereyinstitute.org/courses/Algebra1/COURSE_TEXT_RESOURCE/U12_L2_T2_text_final_es.html
Clase XIV (Viernes 09 de diciembre del 2016)
- Realización de
ejercicios:
Ejercicio 1
Ejercicio 1
En un juego de 40 se reparten 5 cartas
al azar a cada jugada a partir de un mato de 40 cartas. ¿Cuál es la
probabilidad de que jugador tenga:
a) Un dos, un tres, un cuatro, un cinco
del mismo palo
b) 4 cartas del mismo palo
c) Una ronda (3 cartas iguales)
a) P(B)= P(A cualquier palo)·P(2palo
igual A)·P(3igual palo)·P(4igual palo)·P(5igual palo)
P(B)= (4/40) · (1/39) · (1/38) · (1/37) · (1/36) = 5.06*10^-8
b) C: 4 cartas del mismo palo. {A, 2,
3, 4, 5, 6, 7, 8, 9}
P(C)= (4/40) · (9/39) · (8/38) ·
(7/37) = 2.29*10^-4
c) D: Ronda.
P(D)= P(1carta) · P(2da carta= #) · P(3ra carta=#)
P(D)= (1/40) · (3/39) · (2/38) = 1.01*10^-4
Si deseas realizar más ejercicios, dale click AQUÍ.
Jorge C., (2013). Ejercicios de probabilidad de eventos independientes. Recuperado 09 diciembre 2016 de: http://code.jc-mouse.net/posts/apuntes/428/ejercicios-de-probabilidad-de-ev.html
SEGUNDO BIMESTRE
Clase XV (Miércoles 14 de diciembre del 2016)
- Variables Aleatorias Discretas
Una variable aleatoria, X, decimos que es de tipo discreto (conteos) cuando puede tomar los valores x1, ..., xk con probabilidades P(x1), ..., P(xk).
Sean
X: Variable aleatoria
S: Espacio muestral
e: Cualquier elemento de S
x: Valor que puede tomar X
R: Conjunto de los números reales
Entonces
X: S → R Es la correspondencia que establece la variable aleatoria X
e → x, dom X = S, rg X ⊂ R
Cardinalidad: Número de elementos en el S.
- Distribución de probabilidad de una variable aleatoria discreta
Probabilidad de una variable aleatoria discreta
Sea X= variable aleatoria discreta
Entonces P(X=x) representa la probabilidad que la variable X tome el valor x.
La correspondencia que define P(X=x) es una función y se denomina "Distribución de Probabilidad de la variable aleatoria X". Esta correspondencia puede definirse formalmente y ser designada con la notación f:
Distribución de probabilidad de una variable aleatoria discreta X
- Realización de ejemplos y ejercicios
Ejemplo 1:
En un experimento se lanzan tres monedas y se observa el resultado (c: cara o s: sello).
S = {( c, c, c),( c, c, s),( c, s, c),( s, c, c),( c, s, s),( s, c, s),( s, s, c),( s, s, s)}
Describa con una variable, el número de sellos que se obtienen.
Los posibles resultados se los puede representar con una variable. Si X es ésta variable, entonces se dice que X es una variable aleatoria:
X: Variable aleatoria (número de sellos que se obtienen).
Al realizar el experimento, se obtendrá cualquier elemento del espacio muestral S.
Por lo tanto, la variable aleatoria X puede tomar alguno de los números:
x = 0, 1, 2, 3.
Dom X = S Rg X = {0, 1, 2, 3}
Las variables aleatorias pueden representarse con las letras mayúsculas X, Y, ...
Y: Diferencia entre el número de caras y sellos.
Rg Y= { -3, -1, 1, 3 }
Z: El número de caras al cubo, mas el doble del número de sellos, etc.
Rg Z= { 5, 6, 10, 27 }
Para cada variable aleatoria el rango es un subconjunto de los reales.
En el ejemplo, X es una variable aleatoria discreta pues su rango es un subconjunto de los enteros. Además es finita.
- Distribución de probabilidad acumulada de una variable aleatoria discreta
- Ejemplo:
Encuentre la distribución de probabilidad acumulada para el ejemplo de las tres monedas.
Gráfica:
- Propiedades de la Distribución Acumulada para Variables Aleatorias Discretas
1) 0 ≤ F(x )≤1 F es una función de probabilidad
2) a ≤ b ⇒ F(a) ≤ F(b) F es creciente
3) P(X>a) = 1 – P(X≤a) = 1 – F(a) Complemento de Probabilidad
Si deseas conocer más acerca de las variables aleatorias dicretas, dale click AQUÍ.
López, (2013). Variables aleatorias Discretas y sus Distribuciones de Probabilidad. Recuperado 14 diciembre 2016 de:
http://herzog.economia.unam.mx/profesores/blopez/estadistica-discretas.pdf
Clase XVI (Viernes 16 de diciembre del 2016)
- Media y Varizanza de las variables aleatorias discretas
Media
La Media es una medida estadística que describe la tendencia central de una variable aleatoria. Podemos pensar que representa el valor promedio que tomaría la variable aleatoria si el experimento se realizara un gran número de veces en condiciones similares.
Varianza
La Varianza es una medida estadística que cuantifica el nivel de dispersión o variabilidad de los valores la variable aleatoria alrededor de la media.
- Variables aleatorias continuas
Una variable aleatoria X es continua si su función de distribución es una función continua.
En la práctica, se corresponden con variables asociadas con experimentos en los cuales la variable medida puede tomar cualquier valor en un intervalo: mediciones biométricas, intervalos de tiempo, áreas, etc.
- Función de densidad de Probabilidad
La probabilidad de una variable aleatoria continua puede especificarse si existe una función
denominada función de densidad de probabilidad (o simplemente función de densidad), tal
que el área debajo del gráfico de esta función cumpla los requisitos para que sea una medida del valor de probabilidad. Para variables aleatorias discretas, la probabilidad se obtiene de la sumatoria de f(x). En el límite, esta sumatoria se transforma en un integral.
Definición: Función de Densidad de Probabilidad
Sea X una variable aleatoria continua.
Se dice que f es una función de densidad de probabilidad si y solo si,
Si deseas conocer más acerca de la función de densidad de una variable aleatoria continua, dale click AQUÍ.
Alonso Montero, (2013). VARIABLE ALEATORIA Y FUNCIÓN DE
DISTRIBUCIÓN. Recuperado 16 diciembre 2016 de:
http://www.ugr.es/~eues/webgrupo/Docencia/MonteroAlonso/estadisticaII/tema2.pdf
Clase XVII (Miércoles 21 de diciembre del 2016)
- Función de Distribución
Al igual que en el caso discreto se puede definir una función de probabilidad acumulada, la cual en el caso continuo se denomina función de distribución.
Si deseas conocer más acerca de la función variable aleatoria, dale click AQUÍ.
Dagolberto Salgado, (2014). LA FUNCIÓN VARIABLE ALEATORIA . Recuperado 21 diciembre 2016 de: http://www.estadisticacondago.com/images/estadistica_inferencial/VARIABLES%20ALEATORIAS.pdf









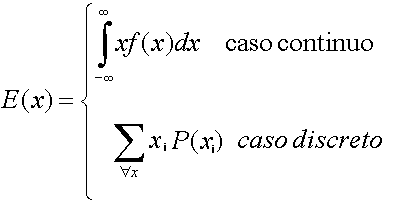



No hay comentarios:
Publicar un comentario